Answer:
The current price is $3000 and price after 9 years from today is $4054.
Explanation:
The future price pt(in dollars) of a certain item can be modeled by the following exponential function
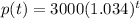
where, t is the number of years from today.
Substitute t=0 to find the current price.
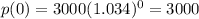
Therefore the current price is $3000.
Substitute t=9 to find the price after 9 years from today.


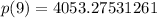
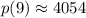
Therefore the price after 9 years from today is $4054.