Answer:
x2 = 0.99
Step-by-step explanation:
from superheated water table
at pressure p1 = 0.6MPa and
temperature 200 degree celcius
h1 = 2850.6 kJ/kg
From energy equation we have following relation
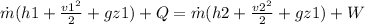
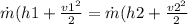
![(h1 + (v1^2)/(2) = (h2 + (v2^2)/(2)</p><p></p><p>[tex]2850.6 + (50^2)/(2) *(1 kJ/kg)/(1000 m^2/s^2) = h2 + (600^2)/(2) *(1 kJ/kg)/(1000 m^2/s^2)](https://img.qammunity.org/2020/formulas/physics/college/2fxya59tu348bxn7bkx54bgp8ws6cw0oey.png)
h2 = 2671.85 kJ/kg
from superheated water table
at pressure p2 = 0.15MPa
specific enthalpy of fluid hf = 467.13 kJ/kg
enthalpy change hfg = 2226.0 kJ/kg
specific enthalpy of the saturated gas hg = 2693.1 kJ/kg
as it can be seen from above value hf>h2>hg, so phase 2 is two phase region. so we have
quality of steam x2
h2 = hf + x2(hfg)
2671.85 = 467.13 +x2*2226.0
x2 = 0.99