Question

Car 1 is 200 m ahead of car 2 on the highway. Car 1 is going 80 kph and car 2 is going 60 kph. Car 2 decides to accelerate at a rate of 1 m/s2 until he catches up. How long will it take to catch up? What will be the car’s final velocity?

Answer 1

It will take 26.32 seconds to catch up, and the Car 2 final velocity is 42.98 m/s (or 154,73 km/h)

Step-by-step explanation:

We have that the Car 1 initial position is X1(0)=200 m, and the Car 2 initial position is X2(0)=0 m. The Car 1 initial speed is V1(0)=80 km/h and Car 2 initial speed is V2(0)=60 km/h. Using the fact that 1 h = 3600 s and 1 km = 1000 m, we have that V1(0)=22.22 m/s (I suggest you always use the International Units System, meters, seconds, Kilograms). Now we can write the equations:

`X(t) = X0 + V0*t+(1)/(2) *t^(2) \\V(t)=V0 + a*t\\\\X1(t)=200 +22.22*t\\X2(t)=0 + 16.66*t + (1)/(2)*t^(2)\\\\`

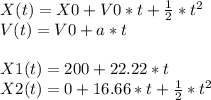
The catch up happens when X1(t)=X2(t):

`0 + 16.66*t + (1)/(2)*t^(2)=200 +22.22*t`

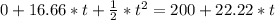
Solving the cuadratic equation we have that t1= -15.2 s and t2=26.32 s. The correct answer of course is t is time, so we have that in 26.32 s the Car 2 catches up Car 1.

Now using this time we find
`V2(t)=16.66 + a*t\\V2(26.32)=16.66 + 1*26.32 = 42.98 m/s`

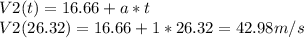
Or 154.73 km/h.