Question

When an air bubble rises from the bottom to the top of a freshwater lake, its volume increases by 70%. If the temperature at the bottom of the lake was 3°C and at the top was 11.5°C, how deep is the lake?

Answer 1

The lake's depth is
`d=6.706 \, m`

Step-by-step explanation:

To find out how deep the lake is, first we must ask ourselves why the volume of the bubble changes. Let's assume ideal gas behaviour. That is:

`P V = nRT`

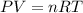
Or we could also put it this way:

`PV/T= nR`

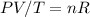
`nR` remains constant (we assume that the number of molecules in the gas doesn't change, no gas is absorbed by the water, and no air is stripped from the water) but
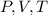`P,V,T` change, they are not the same at the top and at the bottom. V and T change, we know that from the problem's data, but does P change? Yes, it changes because of hydro-static pressure, the deeper we go, the higher the pressure, because of the water column above.

We assume that pressure at the surface is standard atmospheric pressure, 101325 Pa.

Now, we can write:

`P_t\, V_t/T_t= nR\\P_b\, V_b/T_b= nR\\P_t\, V_t/T_t= P_b\, V_b/T_b`

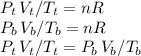
Where b and t stand for bottom and top respectively.

We can solve for
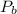`P_b` as follows:

`P_t\, V_t/T_t= P_b\, V_b/T_b\\P_b= P_t \cdot (V_t)/(V_b) (T_b)/(T_t)`

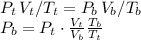
And replacing
`V_t = V_b*1.7` (Because the volume at the top increased 70%) we can calculate
`P_b`

`P_b= 101325\, Pa \cdot 1.7 (276.15\,K)/(284.65 \, K)=167108.82 \,  Pa`

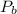
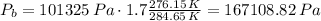
(Note that we use the absolute temperature scale! this is very important)

Now, we know that:

`P_b = P_t +\rho \,g\, d\\d= (P_b -P_t)/\rho\, g`

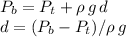
where
`\rho` and
`g` are water's density and gravity's acceleration respectively.
`d` stands for the depth of the lake. Now, water's density changes with temperature, but only slightly in the range of temperatures for this problem (by around 1 in a thousand parts), so we can take the standard value for water density:

`\rho = 1000\, kg/m^3`

Plugging that into the equation we have:

`d= (P_b -P_t)/(\rho\, g) = (65783.82 Pa) / (1000 \, kg/m^3 \cdot 9.81 m/s^2)\\d=6.706 \, m`

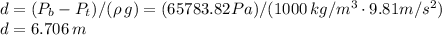
And thus we have found the depth of the lake.