Question

A certain element X has four isotopes. 4.350% of X has a mass of 49.94605 amu. 83.79% of X has a mass of 51.94051 amu. 9.500% of X has a mass of 52.94065 amu. 2.360% of X has a mass of 53.93888 amu. What is the average atomic mass of element X?

Answer 1

Answer: The average atomic mass of the element X is 51.99592 amu

Step-by-step explanation:

Mass of isotope 1 = 49.94605 amu

% abundance of isotope 1 = 4.350% =
`(4.350)/(100)=0.0435`

Mass of isotope 2 = 51.94051 amu.

% abundance of isotope 2 = 83.79% =
`(83.79)/(100)=0.8379`

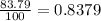
Mass of isotope 3 = 52.94065 amu.

% abundance of isotope 2 = 9.500% =
`(9.500)/(100)=0.095`

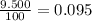
Mass of isotope 4 = 53.93888 amu.

% abundance of isotope 2 = 2.360% =
`(2.360)/(100)=0.0236`

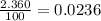
Formula used for average atomic mass of an element :

`\text{ Average atomic mass of an element}=\sum(\text{atomic mass of an isotopes}* {{\text { fractional abundance}})`

`A=(49.94605* 0.0435)+(51.94051 * 0.8379)+ (52.94065* 0.095)+(53.93888* 0.0236)`

`A=51.99592amu`

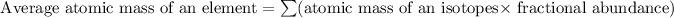
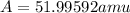
Therefore, the average atomic mass of the element X is 51.99592 amu