Answer:
If Casey is going in the boat's direction, her speed relative to the water is 12 mph in the direction of the boat.
If she is going oposite the boat's direction, her speed relative to the water is 4 mph in the direction of the boat.
If she is going perpendicular to the boat, her speed relative to the water is 8.94 mph in a direction that forms an angle of about 26º with the direction the boat is moving.
Step-by-step explanation:
The speed of Casey with respect with the water depends on the direction she's moving in the deck. The deck has four sides, so there's four possible directions for Casey to move.
Since the water is calm, it's velocity is 0 mph so it doesn't modify the speeds of either Casey or the boat.
Let's consider the boat is moving to the right. That means it's speed with respecto to the water is 8 mph. If we were floating on the water watching from the side the boat and Casey pass by, when she's moving from left to right she seems faster beacuse she's moving in the same direction as the boat and her speed is added to the boats, so it would seem she's walking at 8 mph + 4 mph = 12 mph.
When Casey is moving from riht to left on the deck, she would seem to be moving from left to right at a speed of 4 mph from the water, because the boats speed is higher than hers and is in the opposite direction.
Finally, when she is moving either upwards or downwards, her direction forms a 90º angle with the direction the boat is moving, so her total speed is a vector with horizontal component of 8 mph (going from left to right, the boats speed) and vertical component of 4 mph (with the direction she's moving, either upwards or downwards). By Pythagoras theorem, her velocity would be
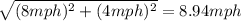and her direction would form an angle of
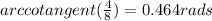with the direction the boat is moving, which is about 26º.