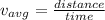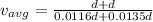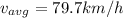Question

You drive on Interstate 10 from San Antonio to Houston, half the time at 54 km/h and the other half at 118 km/h. On the way back you travel half the distance at 54 km/h and the other half at 118 km/h. What is your average speed?

Answer 1

`v_(avg) = 79.7 km/h`

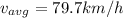
Step-by-step explanation:

As we move from San Antonio to Houston

let the distance is "d" from Antonio to Houston

Half the time it moves with 54 km/h and next half the time it moves 118 km/h

so we will have

`54 T + 118 T = d`

`T = (d)/(172)`

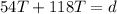
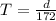
so total time is

`2T = (d)/(86) = 0.0116 d`

now while his return journey half the distance he move with 54 km/h and next half distance with speed 118 km/h

so we have time of return journey

`T' = (d/2)/(54) + (d/2)/(118)`

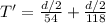
so now we have

`T' = 0.0135 d`

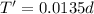
now for the average speed we know that

`v_(avg) = (distance)/(time)`

`v_(avg) = (d + d)/(0.0116 d + 0.0135 d)`

`v_(avg) = 79.7 km/h`

Answer 2

Average speed: 86 km/h

Step-by-step explanation:

Driving from San Antonio to Houston:

1st. half time: 54km/h

2nd. half time: 118 km/h

Average speed = [tex] \frac{54 \frac{km}{h}+ 118 \frac{km}{h} }{2}=86 \frac{km}{h} [\tex]

Driving way back:

1st. half time: 54km/h

2nd. half time: 118 km/h

Average speed = [tex] \frac{54 \frac{km}{h}+ 118 \frac{km}{h} }{2}=86 \frac{km}{h} [\tex]

As in both routes we have the same average speed, then the average speed for the whole trip is 86 km/h