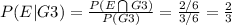Answer:
a.
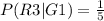
b.
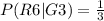
c.
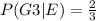
d.
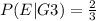
Explanation:
The sample space associated with the random experiment of throwing a dice is is the equiprobable space {R1, R2, R3, R4, R5, R6}. Then,
a. The conditional probability that 3 is rolled given that the roll is greater than 1?
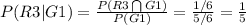
b. What is the conditional probability that 6 is rolled given that the roll is greater than 3?
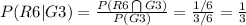
c. What is P [GIE], the conditional probability that the roll is greater than 3 given that the roll is even?
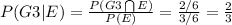
d. Given that the roll is greater than 3, what is the conditional probability that the roll is even?