Answer:
The angular frequencies of all the 3 pendulums shall be same.
Step-by-step explanation:
The time period of a simple pendulum with the approximation
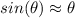 is given by:
is given by:
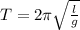
The angular frequency
 is given by
is given by
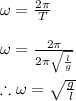
As we can see that the angular frequency is independent on the initial angle (valid strictly for small angle approximations) we conclude that the angular frequencies of the 3 pendulums are the same.