Question

"In analyzing distances by apply ing the physics of gravitational forces, an astronomer has obtained the expression

R= √1/([1/140×10^9 meter]^2 - [1/208×10^9]^2)
Use your calculator to evaluate R. View Available Hint(s)
(A) 3.87 x 10-12 meter
(B) 1.72× 1011 meter
(C) 2.58 x 1011 meter
(D) 1.49 x 1011 meter "

Answer 1

The value of R is
`1.72*10^(11)\ m`.

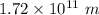(B) is correct option.

Step-by-step explanation:

Given that,

In analyzing distances by apply ing the physics of gravitational forces, an astronomer has obtained the expression

`R=\sqrt{(1)/(((1)/(140*10^(9)))^2-((1)/(208*10^(9)))^2)}`

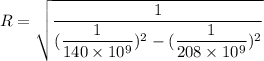
We need to calculate this for value of R

`R=\sqrt{(1)/(((1)/(140*10^(9)))^2-((1)/(208*10^(9)))^2)}`

`R=1.89*10^(11)\ m`

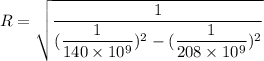
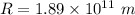
So, The nearest option of the value of R is
`1.72*10^(11)\ m`

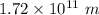
Hence, The value of R is
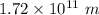`1.72*10^(11)\ m`.