Step-by-step explanation:
Given that,
The vertical motion of mass A is defined by the relation as :
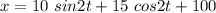
At t = 1 s
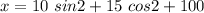
x = 115.33 mm
(a) We know that,
Velocity,
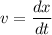
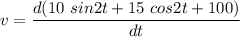
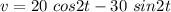
At t = 1 s
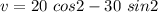
v = 18.94 mm/s
We know that,
Acceleration,
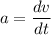
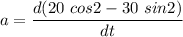
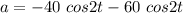
At t = 1 s
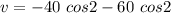
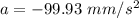
(b) For maximum velocity,

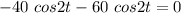
t = 45 seconds
For maximum acceleration,
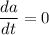

t = 61.8 seconds
Hence, this is the required solution.