Question

If we assume that 60 % of the kinetic energy delivered by a 1.80-kg hammer with a speed of 7.80 m/s is transformed into heat that flows into the nail and does not flow out, what is the temperature increase of an 8.00-g aluminum nail after it is struck ten times?

Answer 1

45.6°C

Step-by-step explanation:

Kinetic energy =
`(1)/(2)mv^2`

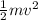
Use m= 1.80kg and v=7.80m/s (mass and speed of hammer).

K = 0,5*1.80kg*(7.80m/s)^2 = K=54.8J

Heat is 60% of Kinetic energy. Q = 0.6*54.8J = 32.9J

As it is stuck 10 times the total heat is 10*32.9J = Total Heat = 329J

Use the equation
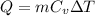`Q = mC_v \Delta T` to find change of temperature:

`\Delta T = (Q)/(mC_v)`

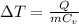
Q = 329J; m = 8.00g of aluminium; C_v = 0.900J/g°C (For aluminium)

`\Delta T = (329J)/(8.00g*0.900J/g°C)`

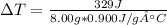
Calculating gives Change of Temperature = 45.6°C