Question

Each day, X arrives at point A between 8:00 and 9:00 a.m., his times of arrival being uniformly distributed. Y arrives independently of X between 8:30 and 9:00 a.m., his times of arrival also being uniformly distributed. What is the probability that Y arrives before X?

Answer 1

Y will arrive earlier than X one fourth of times.

Explanation:

To solve this, we might notice that given that both events are independent of each other, the joint probability density function is the product of X and Y's probability density functions. For an uniformly distributed density function, we have that:

`f_X(x) = (1)/(L)`

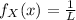
Where L stands for the length of the interval over which the variable is distributed.

Now, as X is distributed over a 1 hour interval, and Y is distributed over a 0.5 hour interval, we have:

`f_X(x) = 1\\\\f_Y(y)=2`.

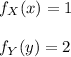Now, the probability of an event is equal to the integral of the density probability function:

`\iint_A f_(X,Y) (x,y) dx\, dy`

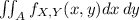
Where A is the in which the event happens, in this case, the region in which Y<X (Y arrives before X)

It's useful to draw a diagram here, I have attached one in which you can see the integration region.

You can see there a box, that represents all possible outcomes for Y and X. There's a diagonal coming from the box's upper right corner, that diagonal represents the cases in which both X and Y arrive at the same time, under that line we have that Y arrives before X, that is our integration region.

Let's set up the integration:

`\iint_A f_(X,Y) (x,y) dx\, dy\\\\\iint_A f_(X) (x) \, f_(Y) (y) dx\, dy\\\\2 \iint_A  dx\, dy`

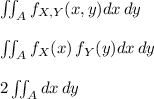
We have used here both the independence of the events and the uniformity of distributions, we take the 2 out because it's just a constant and now we just need to integrate. But the function we are integrating is just a 1! So we can take the integral as just the area of the integration region. From the diagram we can see that the region is a triangle of height 0.5 and base 0.5. thus the integral becomes:

`2 \iint_A  dx\, dy= 2 * (0.5 * 0.5 )/(2) \\\\2 \iint_A  dx\, dy= (1)/(4)`

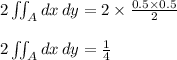
That means that one in four times Y will arrive earlier than X. This result can also be seen clearly on the diagram, where we can see that the triangle is a fourth of the rectangle.