Question

A shoe manufacturer collected data regarding men's shoe sizes and found that the distribution of sizes exactly fits the normal curve. If the mean shoe size is 11 and the standard deviation is 1.5, find:a) What percent of male shoe sizes are greater than 8?

Answer 1

Answer: 97.72%

Explanation:

Given : A shoe manufacturer collected data regarding men's shoe sizes and found that the distribution of sizes exactly fits the normal curve.

Let x be the random variable that represents the shoe sizees.

Also, The population mean =
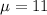`\mu=11` ; Standard deviation:
`\sigma=1.5`

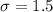
Formula for z:-

`z=(x-\mu)/(\sigma)`

Put x= 8, we get

`z=(8-11)/(1.5)=-2`

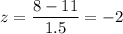
Now, the probability that the male shoe sizes are greater than 8 :-

`P(x>8)=P(z>-2)=1-P(z\leq-2)\\\\=1-0.0227501=0.9772499\approx0.9772`

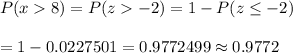
Hence, the percent of male shoe sizes are greater than 8 is 97.72%.