Answer:
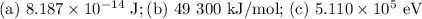
Step-by-step explanation:
This question involves the conversion of mass into energy: E = mc².
e + p ⟶ γ + γ
Each particle has the same mass so, in terms of mass, we can write
2e ⟶ 2γ or
e ⟶ γ
Thus, we can just convert the mass of an electron to its energy equivalent.
(a) Energy in joules
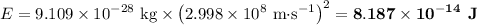
(b) Energy in kilojoules per mole

(c) Energy in electron volts
