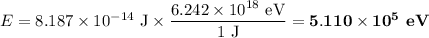Question

Consider a process in which two gamma-ray photons are released when an electron and a positron are annihilated. [Note that the mass of a positron is equal to that of an electron, and the gamma-ray photon has no mass.]

(a) What is the final energy of each photon (in J units)?
(b) What is the final energy of each photon (in kJ/mol units)?
(c) What is the final energy of each photon (in eV units)?

Answer 1

`\text{(a) }8.187 * 10^(-14)\text{ J}; \text{(b) 49 300 kJ/mol; (c) } 5.110 * 10^(5)\text{ eV}`

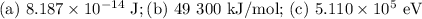
Step-by-step explanation:

This question involves the conversion of mass into energy: E = mc².

e + p ⟶ γ + γ

Each particle has the same mass so, in terms of mass, we can write

2e ⟶ 2γ or

e ⟶ γ

Thus, we can just convert the mass of an electron to its energy equivalent.

(a) Energy in joules

`E= 9.109 * 10^(-28)\text{ kg} * \left (2.998 * 10^(8)\text{ m$\cdot$s}^(-1)\right )^(2) = \mathbf{8.187 * 10^(-14)}\textbf{ J}`

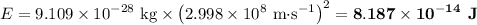
(b) Energy in kilojoules per mole

`E =8.187 * 10^(-14)\text{ J } * \frac{\text{ 1 k}}{\text{1000 J}} \,* \,\frac{6.022 * 10^(23)}{\text{1 mol}} = 4.930 * 10^(7)\text{ J/mol}= \textbf{49 300 kJ/mol}`

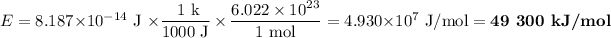
(c) Energy in electron volts

`E = 8.187 * 10^(-14)\text{ J}* \frac{6.242 * 10^(18)\text{ eV}}{\text{1 J}} = \mathbf{5.110 * 10^(5)}\textbf{ eV}`