Answer: The required scale factor of dilation is 3.
Step-by-step explanation: Given that the dashed triangle is the image of the solid triangle and the center of dilation is (-4, -4).
We are to find the scale factor that is used to create the dilation.
We know that the scale factor of dilation is given by

From the graph, we note that
two vertices of the original triangle are (-4, -4) and (-4, -6).
And, the corresponding two vertices of the dilated triangle are (-4, -4)and (-4, 2).
So, the length of a side of the original triangle, as calculated using distance formula is
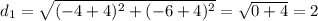
and the length of the corresponding side of the dilated triangle is

Therefore, the scale factor of dilation is
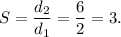
Thus, the required scale factor of dilation is 3.