Step-by-step explanation:
The given reaction will be as follows.
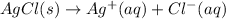 ............. (1)
............. (1)
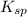 =
=
![[Ag^(+)][Cl^(-)] = 1.8 * 10^(-10)](https://img.qammunity.org/2020/formulas/chemistry/college/19r5y0zy1oy5i901u3yhc2x9eeqfnfntpo.png)
Reaction for the complex formation is as follows.
![Ag^(+)(aq) + 2NH_(3)(aq) \rightleftharpoons [Ag(NH_(3))_(2)]^(+)(aq)](https://img.qammunity.org/2020/formulas/chemistry/college/yl3nvd0t54as42wobez3hbs61f54kdzbnj.png) ........... (2)
........... (2)
 =
=
![([Ag(NH_(3))_(2)])/([Ag^(+)][NH_(3)]^(2)) = 1.0 * 10^(8)](https://img.qammunity.org/2020/formulas/chemistry/college/prvchg4kgxab3rcdg38zpft2qxw30ixnl4.png)
When we add both equations (1) and (2) then the resultant equation is as follows.
![AgCl(s) + 2NH_(3)(aq) \rightarrow [Ag(NH_(3))_(2)]^(+)(aq) + Cl^(-)(aq)](https://img.qammunity.org/2020/formulas/chemistry/college/oklftxn3sslmtd6pvx6go0jbf6xukwgaxj.png) ............. (3)
............. (3)
Therefore, equilibrium constant will be as follows.
K =

=
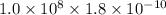
=
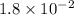
Since, we need 0.010 mol of AgCl to be soluble in 1 liter of solution after after addition of
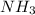 for complexation. This means we have to set
for complexation. This means we have to set
![[Ag^(+)]](https://img.qammunity.org/2020/formulas/chemistry/college/h1nns1d0qnziktvpw4fd4yxw7t2js546dn.png) =
=
![[Cl^(-)]](https://img.qammunity.org/2020/formulas/chemistry/college/kcmcc4pimrtq309100ji6r3lasvatuk47z.png)
=
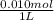
= 0.010 M
For the net reaction,
![AgCl(s) + 2NH_(3)(aq) \rightarrow [Ag(NH_(3))_(2)]^(+)(aq) + Cl^(-)(aq)](https://img.qammunity.org/2020/formulas/chemistry/college/oklftxn3sslmtd6pvx6go0jbf6xukwgaxj.png)
Initial : 0.010 x 0 0
Change : -0.010 -0.020 +0.010 +0.010
Equilibrium : 0 x - 0.020 0.010 0.010
Hence, the equilibrium constant expression for this is as follows.
K =
![([Ag(NH_(3))^(+)_(2)][Cl^(-)])/([NH_(3)]^(2))](https://img.qammunity.org/2020/formulas/chemistry/college/fgom5h2hhgkyt1bxbmta0sku8efkwgmu98.png)
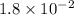 =
=
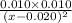
x = 0.0945 mol
or, x = 0.095 mol (approx)
Thus, we can conclude that the number of moles of
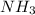 needed to be added is 0.095 mol.
needed to be added is 0.095 mol.