Question

Suppose that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. After hours of burning, a candle has a height of centimeters. After hours of burning, its height is centimeters. What is the height of the candle after hours?

Answer 1

h = a + b * t, this equation gives you the height of the candle after t hours, where:

h = height of the candle

t = hours of burning

a = the y intercept

b = the slope

Explanation:

In your problem says that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. This means that the independent variable is t (hours of burning) and the dependent variable is h (height of the candle).

A linear function has the following form:

y = f(x) = a + bx

a is the constant term or the y intercept. It is the value of the dependent variable when x = 0.

b is the coefficient of the independent variable. It is also known as the slope and gives the rate of change of the dependent variable.

NOTE:

In order to find numerical values you need at least two points in order to find the slope (t1,h1), (t2,h2), with this equation:

b =
`(h_(2) - h_(1))/(t_(2) - t_(1)\\ ) \\`

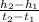
Next you find a when x = 0, y = a, where y is one of the points that you want to evaluate.

With these values you put them in this equation h = a + b * t and that's it! You will find the height of the candle after t hours.