Question

Suppose a worker needs to process 100 items. The time to process each item is exponentially distributed with a mean of 1 minute, and the processing times are independent. Approximately, what is the probability that the worker finishes in less than 2.25 hours?

Answer 1

Answer: 0.0368

Explanation:

The cumulative distribution function for exponential distribution is :-

`P(x)=1-e^(-\lambda x)`

, where
`\lambda` is the mean of the distribution.

Given : The time to process each item is exponentially distributed with a mean of 1 minute .

In hour, the mean time to process each item =
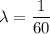`\lambda=(1)/(60)` hour

Then , the probability that the worker finishes in less than 2.25 hours :-

`P(x<2.25)=1-e^{-(1)/(60) *2.25}\\\\\approx1-0.9632=0.0368`

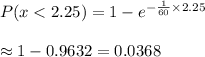
Hence, the probability that the worker finishes in less than 2.25 hours = 0.0368