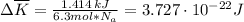Question

The temperature of 6.30 mol of an ideal monatomic gas is raised 18.0 K in an adiabatic process. What are (a) the work W done by the gas, (b) the energy transferred as heat Q, (c) the change ΔEint in internal energy of the gas, and (d) the change ΔK in the average kinetic energy per atom?

Answer 1

a) The work done by the gas is
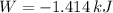`W=-1.414\,kJ`, that means, work is done on the gas, not viceversa.

b)
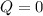`Q=0` because it is an adiabatic process.

c)
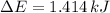
`\Delta E=1.414\,kJ`

d)
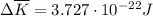`\Delta\overline K= 3.727\cdot 10^(-22)J` per atom

Step-by-step explanation:

First, for an ideal monoatomic gas we have:
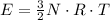`E= (3)/(2)N\cdot R\cdot T`, This result can be experimentally verified or derived from statistical mechanics.

From which we can see that:
`c_v=(\partial e)/(\partial T)=(3)/(2)R`

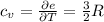
An adiabatic process is one in which no heat is transferred to or from the system, therefore the first law can be written as:

`\Delta E =-W`

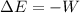
we can calculate
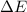`\Delta E` as follows:

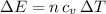`\Delta E= n\,c_v \, \Delta T` which follows from our first equation.

`\\\Delta E= n\, (3)/(2)R  \, \Delta T \\ \\ \Delta E= 6.3\, mol\, (3)/(2)\,8.314(J)/(K mol)   \,  18K\\ \\ \Delta E=-W=1.414\,kJ`

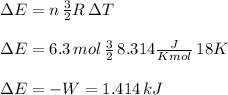
Thus the gas doesn't do any work, on the contrary, work is done on the gas to compress it.

As a monoatomic gas can only store energy in kinetic energy form, we have that the change in internal energy is related to the change in kinetic energy.

`E = n*N_a *\overline K`

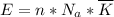
So:

`(\Delta E)/(N) =\Delta \overline K`

`\Delta\overline K= (1.414\, kJ)/(6.3mol*N_a) =3.727\cdot 10^(-22)J`