Question

Find the volume of the S if the base of S is an elliptical region with boundary curve 9x^2 + 4y^2 = 36 . Cross sections perpendicular to the x-axis are isosceles right triangles with hypotenuse in the base.

Answer 1

The volume of the solid S is: 24

Step-by-step explanation:

Observe attached a sketch of the situation. The triangle represents one cross section, one of the isosceles triangles.

Notice the hypotenuse length is 2y. We can get the length of the legs b by using the Pythagorean theorem:

`b^2+b^2=(2y)^2\to 2b^2=4y^2\to b^2=2y^2`

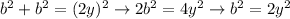
I did not solve the equation for b since it will be useful to have b squared.

We need the volume of the cross sections. It is the area of the triangle multiplied by its thickness dx.

The area of the triangle is half of its base times its height, both base and height are b (the legs of the right triangle), thus:

`A=\displaystyle(b\cdot b)/(2)=(b^2)/(2)`

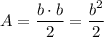
Replacing b squared by the expression we got for it in terms of y:

`A=\displaystyle(2y^2)/(2)=y^2`

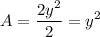
Therefore the volume of a cross section is:
`dV=y^2\,dx`

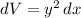
We can get y squared in terms of x by solving the ellipse equation:

`9x^2+4y^2=36\to 4y^2=36-9x^2\to \displaystyle y^2=9-(9)/(4)x^2`

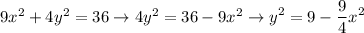
Therefore, the volume of the cross section is:

`\displaystyle dV= (9-(9)/(4)x^2)\,dx`

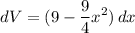
To get the limits of the integral, notice they are the x-intercepts of the ellipse. We get them by plugging y=0 into the ellipse equation to get:

`9x^2=36\to x^2=4\to x=\pm2`

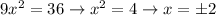
Therefore the integral for the volume is:

`V=\displaystyle\int_(-2)^(2)(9-(9)/(4)x^2)\,dx`

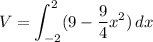
We solve it using the basic rule:

`\displaystyle V=9x-(9)/(4)\cdot(1)/(3)x^3\Bigg|_(-2)^(2)\\[0.2in]\displaystyle V=\left(9(2)-(3)/(4)(2)^3\right)- \left(9(-2)-(3)/(4)(-2)^3\right)\\[0.2in]\displaystyle V=(18-6)-(-18+6)=24`