(a). The average speed of the particle in the interval
![[1,2]](https://img.qammunity.org/2020/formulas/physics/high-school/704m0je92wrc8l7ubdnu123zb0n2jnu6rf.png) is
is
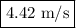 .
.
(b). The average speed of the particle in the interval
![[1,1.5]](https://img.qammunity.org/2020/formulas/physics/high-school/s8pn9glbovhldec9sv1c7r1la590vubyhd.png) is
is
 .
.
Further Explanation:
The position of the particle on the surface of mars is given by:
 .
.
The average speed of the particle is given as:
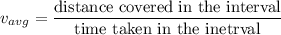
Part (a):
The average speed of the particle in the interval
![\bf[1,2]](https://img.qammunity.org/2020/formulas/physics/high-school/mcs9pzx5224ayze1pp0q9yuq2oxy6imr8b.png) ,
,
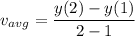
Now,

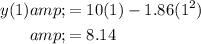
Substitute the values in above expression of
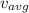 :
:
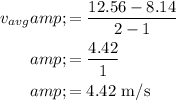
So, the average speed of the particle in the interval
![[1,2]](https://img.qammunity.org/2020/formulas/physics/high-school/704m0je92wrc8l7ubdnu123zb0n2jnu6rf.png) is
is
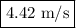 .
.
Part (b):
The average speed of the particle in the interval
![\bf[1,1.5]](https://img.qammunity.org/2020/formulas/physics/high-school/wvaiwf0v7uzfhp448ufjgdjyly80pxrkyg.png) ,
,
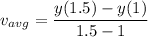
Now,

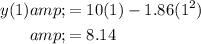
Substitute the values in above expression of
 :
:
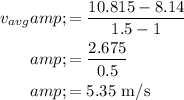
So, the average speed of the particle in the interval
![[1,1.5]](https://img.qammunity.org/2020/formulas/physics/high-school/s8pn9glbovhldec9sv1c7r1la590vubyhd.png) is
is
 .
.