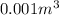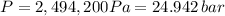Question

Consider the gaseous reaction, X(g) + Y(g) →XY(g) A mixture of 0.8 mole of gas X and 1 mole of gas Y was allowed to react at 300 K and 1 L sealed container. At the end of the reaction, what is the total pressure of the mixture? The temperature and volume remains constant during the reaction.

Answer 1

The final pressure is 2494200 Pa or 24.942 bar

Step-by-step explanation:

Assuming that the reaction goes to completion, and that the gases have ideal gas behaviour, we can find the pressure after the reaction has taken place.

We know that for ideal gases we have:

`P\cdot V = n\cdot R \cdot T`

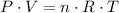
or:

`P = ( n\cdot R \cdot T)/(V)`

Where:

• P is the absolute pressure
• n is the total number of mols (of all gases present)
• R is the ideal gas constant (
  `8.314 \: (J)/(K\cdot mol)` in SI units)
• T is the absolute Temperature
• V is the volume

Now, we know that T and V remain constant, and R is just a constant, thus we only need to find out what n is after the reaction has taken place.

We know that at the onset, we have 0.8 mol of X, and 1 mol of Y. moreover, the reaction is:

`X(g)+Y(g)\rightarrow XY(g)`

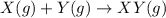
We see that for every mol of XY that is formed, 1 mol of X and 1 mol of Y is consumed. Thats only what the stoichiometry of the reaction tells us, but we need to know how many mols ox X and Y actually react! To find out, we need to look at how much X and Y is present, and which reactant will be the first to run out.

If all the mols of Y reacted to with X to form XY, we would need 1 mol of X, because we have 1 mol of Y, and every mol of Y reacts with 1 mol of X. But we don't have 1 mol of X, we only have 0.8 mols of X.

Thus, we come to the conclusion that only 0.8 mols of both X and Y will react with each other, to form 0.8 mols of XY.

So, we have now 0.8 mols of XY, and 0 mols of X, given that all of them reacted to form XY, But we still have 0.2 mols of Y left unreacted! in short:

Initial quantities:

X= 0.8 mol

Y= 1 mol

XY= 0 mol

then, 0.8 mols of both X and Y react to form 0.8 mols of XY

and thus, the inal amounts are:

`X= 0.8 - 0.8 = 0 \: mol`

`Y= 1 - 0.8 =0.2 \: mol`

`XY = 0 + 0.8 \: mol`

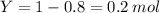
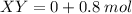
Total:

`n=0+0.2+0.8 = 1 \: mol`

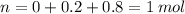
Now we only need to insert this value into our original ideal gas law equation, and we get our desired result, take into account that 1 L is equal to
`0.001 m^3`

`P = ( n\cdot R \cdot T)/(V)`

`P = ( 1mol\cdot 8.314 (J)/(K \cdot mol) \: \cdot 300K)/(0.001 m^3)`

`P= 2,494,200 Pa = 24.942 \, bar`