Question

An archer fires an arrow, which produces a muffled "thwok" as it hits a target. If the archer hears the "thwok" exactly 1 s after firing the arrow and the average speed of the arrow was 40 mis, what was the distance separating the archer and the target? Use 340 m/ s for the speed of sound.

Answer 1

35,79 meters

Step-by-step explanation:

So, we got an archer, and we got a target. Lets call the distance between this two d.

Now, the archer fires the arrow, that, in a time
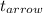`t_(arrow)` travels the distance d with a speed
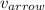`v_(arrow)` of 40 m/s and hits the target. We can see that the equation will be:

`v_(arrow) * t_(arrow) = d\\ \\40 (m)/(s) * t_(arrow) = d`

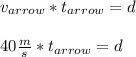
Immediately after this, the arrow produces a muffled sound, which will travel the distance d at 340 m/s in a time
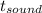`t_(sound)`. Obtaining :

`v_(sound) * t_(sound) = d\\ \\340 (m)/(s) * t_(sound) = d`.

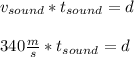Finally, the sound reaches the archer, exactly 1 second after he fired the bow, so:

`t_(arrow) + t _(sound) = 1 s`.

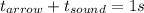This equation allows us to write:

`t _(sound) = 1 s - t_(arrow)`.

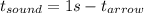Plugging this relationship in the distance equation for the sound:

`340 (m)/(s) * t_(sound) = d \\ \\ 340 (m)/(s) * (1 s- t_(arrow)) = d`.

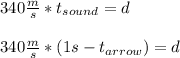Now, we can replace d from the first equation, and obtain:

`40 (m)/(s) * t_(arrow) = d \\ 40 (m)/(s) * t_(arrow) = 340 (m)/(s) * (1 s- t_(arrow))`.

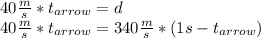Now, we can just work a little bit:

`40 (m)/(s) * t_(arrow) = 340 (m)/(s) * 1 s - 340 (m)/(s) * t_(arrow) \\ \\ 40 (m)/(s) * t_(arrow) + 340 (m)/(s) * t_(arrow) = 340 m \\ \\ 380 (m)/(s) * t_(arrow) = 340 m \\ \\ t_(arrow) = (340 m)/(380 (m)/(s)) \\ \\ t_(arrow) = 0.8947 s`.

Now, we can just plug this value into the first equation:

`40 (m)/(s) * t_(arrow) = d`

`40 (m)/(s) * 340/380 s = 35,79 s = d`