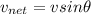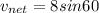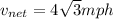Question

A boat travels at 8 miles an hour in still water. At what angle with the shore must the boat be steered to reach a point directly opposite the starting point if the velocity of the current is 4 mi/hr. What is the resultant velocity of the boat with respect to the shore.?

Answer 1

`v_(net) = 4\sqrt3 mph`

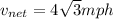
Step-by-step explanation:

Since we know that the displacement of the boat in the direction of flow of the river must be zero

so we have to at such an angle with shore so that the component of velocity of boat along the direction of flow must be equal and opposite to the flow velocity of the water

so we will have

`v cos\theta + v_r = 0`

`8 mph cos\theta + 4 mph = 0`

`cos\theta = -(4 mph)/(8 mph)`

`cos\theta = -0.5`

`\theta = 120 ^o`

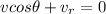
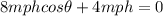
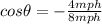
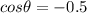
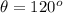
Now the resultant velocity of the boat is in perpendicular to the flow of water

so we will have

`v_(net) = v sin\theta`

`v_(net) = 8 sin60`

`v_(net) = 4\sqrt3 mph`