Proof with Step-by-step explanation:
From the Newton's law of viscosity we have
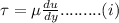
where
 is the wall shear stress
is the wall shear stress
 is the coefficient of dynamic viscosity
is the coefficient of dynamic viscosity
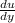 is the velocity gradient in the flow
is the velocity gradient in the flow
Now from the principle of boundary layer condition we know that the velocity of the fluid that is in contact with a surface the velocity of the fluid is same as that of the boundary itself.
Hence from the attached figure we can infer that
Velocity at
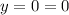
Velocity at
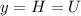
Solving equation 'i' we get

from the boundary conditions we obtain that c = 0 since

Also we have
