Question

In a hearing test, subjects estimate the loudness (in decibels) of a sound, and the results are (mean = 70): 68, 67, 70, 71, 68, 75, 68, 62, 80, 73, 68. What is the sample standard deviation?

Answer 1

4.5126 approximately 4.5

Explanation:

First of all, we need to identify the type of data that we are receiving, in this case we got a finite amount of data, a discrete set of data, 11 of them to be precise, so the first parameter: the size of the sample (N) is equal to 11.

So, for this problem we goin' to use the formula for standard deviation for discrete variables that it's given by: see the attached image

where σ correspond to the standard deviation, μ correspond to the mean (in this case μ = 70 decibels) , xi correspond to each of the data values and i correspond to a counter beginning in i=1 with x1 = 68 and ending in i=N=11 (the size of the sample) with x11=68.

Finally we operate using the formula and we obtain that the standard deviation of this sample is equal to 4.5126

Answer 2

4.73

Explanation:

We have 11 subjects who took the hearing test and the mean this group got was 70.

To find the standard deviation we need to follow the next steps:

1. First we calculate the mean of the sample

In this case we already know that the mean is 70.

2. We calculate the variance for each data, to do this we need to subtract the value of the data from the mean:

Now, with the data we got we get:

70 - 68 = 2

70 - 67 = 3

70- 70 = 0

70 - 71 = -1

70 - 68 = 2

70 - 75 = -5

70 - 68 = 2

70 - 62 = 8

70 - 80 = -10

70 - 73 = -3

70 - 68 = 2

3. Now we are going to take each of the resulting values, square them and then sum them up:

`2^(2) +3^(2) +0^(2) +(-1)^(2) +2^(2) +(-5)^(2) +2^(2)  +8^(2) +(-10)^(2) + (-3)^(2) +2^(2) \\=4+9+0+1+4+25+4+64+100+9+4= 224`

4. Now, we're going to divide this result by the number of data points less one (in this case we will divide by 10)

224/10 = 22.4

This 22.4 is the variance.

5. To find the standard deviation, we are going to take the square root of the variance:

`√(22.4) = 4.73`

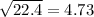
Therefore, the standard deviation is 4.73