Answer:
The final displacement is: R=12.74m, 38.85° West of North.
Step-by-step explanation:
The very first thing we need to do when solving this problem is to draw a diagram that will represent the vectors. The diagram doesn't have to be perfect (unless you are solving this graphically) it will just help us determine how to work the vectors up. (Refer to attached diagram).
Once we got our diagram, we can start finding our components of the vectors relative to where the angles are located at. For vector A we got our components to be:
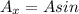 θ
θ
in this case we use sin because the angle is oposite to side x of the vector. So now we can substitute values in.


Now, for the y-component we follow the same procedure but we use cos instead of sin, like this:
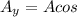 θ
θ
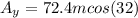

We can follow the same procedure for the x- and y- components of vectors B and C.
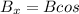 θ
θ


Notice how in this case the x-component will be negative. This means that the vector goes to the left, just as indicated by the diagram we drew before.
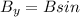 θ
θ

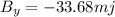
Again, the y-component is negative, meaning that the vertical component of the vector will go downwards according to the diagram.
And for C we get:
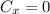
and
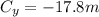
As we can see in the diagram.
So once we got the components for our vectors we can add them to get the resulting vector:

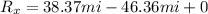

And we do the same for the y-components:
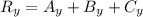
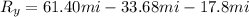

So we got our resulting vector to be:
![R=R_(x)+R_{y]](https://img.qammunity.org/2020/formulas/physics/high-school/lpm2t01erkgek54ni3mgw7f1oqsnpft2vt.png)
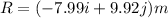
Which can now be used to find the magnitude and direction of our vector. The magnitude can be found by using pythagore and the displacement coefficients, like this:

so:

which yields:
|R|=12.74m
And the angle is found by using the function tan:
 θ
θ
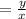
 θ
θ
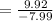
 θ
θ
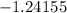
So finaly:
θ=
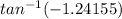
θ= -51.15
but be careful to pick the rigth quadrant, you can do so by looking at the diagram we originally drew. You may see it goes upwards to the right, so the angle must be located on the second quadrant, which means the angle will be at: 180°-51.15°=128.85°
or 38.85° West of North.
So de magnitude of the sum of vectors is 12.74m with an angle of 38.85° west of north.