Question

A line of charge starts at x = +x0 and extends to positive infinity. The linear charge density is λ = λ0x0/x. Determine the electric field at the origin. (Use ke, λ0, and x0 as necessary.)

Answer 1

`E=-K_e(\lambda_0 )/(2x_0)N/C`

Step-by-step explanation:

We know that electric field given as

`E=K_e\int_(x_1)^(x_2)(\lambda )/(x^2)dx`

Here given that

`\lambda =(\lambda _0x_0)/(x)`

So

`E=K_e\int_(x_1)^(x_2)(\lambda_0x_0 )/(x^3)dx`

`E=K_e\int_(x_0)^(\infty )(\lambda_0x_0 )/(x^3)dx`

Now by integrating we get

`E=-K_e\lambda_0\left [ (1 )/(2x^2) \right ]^(\infty )_x_0dx`

`E=-K_e(\lambda_0 )/(2x_0)dx`

So the electric field at the origin E

`E=-K_e(\lambda_0 )/(2x_0)N/C`

Answer 2

Step-by-step explanation:

it is given that, the linear charge density of a charge,
`\lambda=(\lambda_ox_o)/(x)`

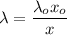
Firstly, we can define the electric field for a small element and then integrate for the whole. The very small electric field is given by :

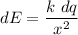`dE=(k\ dq)/(x^2)`..........(1)

The linear charge density is given by :

`\lambda=(dq)/(dx)`

`dq=\lambda.dx=(\lambda_ox_o)/(x)dx`

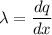
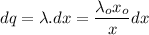
Integrating equation (1) from x = x₀ to x = infinity

`E=\int\limits^\infty_(x_o) {(k\lambda_ox_o)/(x^3)}.dx`

`E=-(k\lambda_ox_o)/(2)(1)/(x^2)|_(x_o)^\infty}`

`E=(k\lambda_o)/(2x_o)`

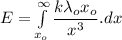
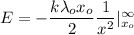
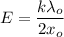
Hence, this is the required solution.