Question

(a) Assume the equation x = At3 + Bt describes the motion of a particular object, with x having the dimension of length and t having the dimension of time. Determine the dimensions of the constants A and B. (Use the following as necessary: L and T, where L is the unit of length and T is the unit of time.)

Answer 1

The dimension of A is L/T^3 and the dimension of B is L/T

Explanation:

We can write the equation but just in terms of its dimensions and work with dimension analysis to find the dimensions of the constants.

Writing the dimensions equation.

For the given equation

`x = At^3+Bt`

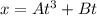
We can write

`[x]=[A][t]^3+[B][t]`

We can then replace the dimensions where x is a length dimension which means
`[x]=L` and t has a time dimension,
`[t] = T`, so we get

`L = [A]T^3+[B]T`

Since we are adding terms on the right side both terms must have the same dimension. That means we have

`[A]T^3=L`

And

`[B]T=L`

Finding the dimensions of A and B

We can finally solve for the dimensions of each.

For A we have

`[A]T^3=L\\`

Solving for [A] will give us

`\boxed{[A] = \cfrac{L}{T^3}}`

Solving for [B]

`[B]T=L`

`\boxed{[B]=\cfrac LT}`