Question

To furnish a room in a model home, an interior decorator is to select 2 chairs and 2 tables from a collection of chairs and tables in a warehouse that are all different from each other. If there are 5 chairs in the warehouse and if 150 different combinations are possible, how many tables are in the warehouse?

Answer 1

The number of tables in the warehouse are:

6

Explanation:

We know that the method of combination is used to find the number of combinations possible in order to select r items from a set of n items

and is given by:

`n_C_r=(n!)/(r!* (n-r)!)`

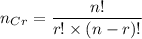
Now, it is given that:

In order to furnish a room we have to select 2 chairs and 2 tables from 5 chairs and let there are t tables.

Also, the total number of combinations possible are: 150

i.e.

`5_C_2* t_C_2=150\\\\i.e.\\\\(5!)/(2!* (5-2)!)* (t!)/(2!* (t-2)!)=150\\\\(5!)/(2!* 3!)* (t(t-1)(t-2)!)/(2* (t-2)!)=150\\\\10* (t(t-1))/(2)=150\\\\5t(t-1)=150\\\\t(t-1)=30\\\\t^2-t-30=0\\\\t^2-6t+5t-30=0\\\\t(t-6)+5(t-6)=0\\\\(t+5)(t-6)=0\\\\i.e.\\\\t=-5\ or\ t=6`

But the number of table can't be negative.

Hence, we get:

`t=6`

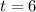
There are 6 tables in the warehouse.