Question

A stuntman sitting on a tree limb wishes to drop vertically onto a horse galloping under the tree. The constant speed of the horse is 11.0 m/s, and the man is initially 2.45 m above the level of the saddle. (a) What must be the horizontal distance between the saddle and limb when the man makes his move?

Answer 1

7.78 meters

Step-by-step explanation:

So, lets just pretend we are working in a vacuum, like in (almost) all physics problems. So, we must find how much time will take to the man fall the height to the saddle to know how far away must be the saddle to be right under the limb at the right time.

So, we can use kinematics relationships. We know the for a 1D movement, with constant acceleration, the equation its:

`y(t) \ = \ y_0 \ + \ v_0 \ * \ t \ +(1)/(2) \ a \ t^2`

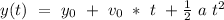
For our problem, the initial position its the height from which the man jumps,

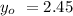`y_o \ = 2.45 \m`, the final position

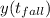`y(t_(fall))` must be the level of the saddle

`y(t_(fall)) \ = 0 \ m`,

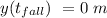the initial velocity must be

`v_0 \ = \ 0 \ (m)/(s)`,

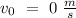and the acceleration its the gravitational pull,

`a \ = \ - \ g \ = \ - \ 9.8 \ (m)/(s^2)`.

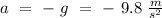So, we get:

`0\ = \ 2.45 \ m \ + \ 0 \ * \ t \ - (1)/(2) \ g \ t_(fall)^2`

`0\ = \ 2.45 \ m \ - (1)/(2) \ g \ t_(fall)^2`

`- \ 2.45 \ m \ = - (1)/(2) \ g \ t_(fall)^2`

`\ 2.45 \ m \ = (1)/(2) \ g \ t_(fall)^2`

`2 \ * \ 2.45 \ m \ = \ g \ t_(fall)^2`

`( 2 \ * \ 2.45 \ m)/(g) \ = t_(fall)^2`

`\sqrt{ ( 2 \ * \ 2.45 \ m)/(g) } \ = \ t_(fall)`

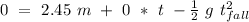
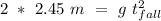
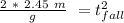
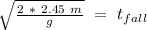
So, we can calculate this an get

`t_(fall) \ = \sqrt{ ( 2 \ * \ 2.45 \ m)/(9.8 (m)/(s^2) ) }`

`t_(fall) \ = \sqrt{ (1)/(2) }`

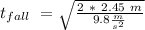
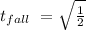
Now, we know how much time will take for the man to fall to the level of the saddle. If the horse is galloping to a constant speed of

`v_h \ = \ 11.0 \ (m)/(s)`,

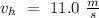in the time
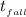`t__(fall)` the horse travels a distance

`d_h \ = \ v_h * t_(fall)`

`d_h \ = \ 11.0  \ (m)/(s) * \sqrt{ (1)/(2) }`

`d_h \ = \ 7.78 \ m`

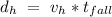
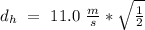
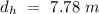
And this must be the distance we are looking for. So, the saddle and the limb must be at 7.78 meters when the man makes his move.