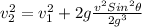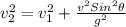Answer:
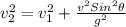
Step-by-step explanation:
Case I:
initial velocity, u = 0 m/s
Final velocity, v' = v Sinθ /g
Height = h
acceleration = g
Use third equation of motion, we get
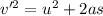
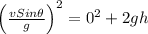
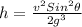 . ... (1)
. ... (1)
Case II:
initial velocity, u = v1
Final velocity, v = v2
height = h
acceleration due to gravity = g
Use third equation of motion, we get
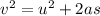
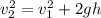
Substitute the value of h from equation (1) ,we get