Answer:
A cell phone provider charges $30 each month.
It costs $0.05 for every minute of talk and $0.10 for every text sent. There is no charge for receiving texts.
Part A:
Let t represents the number of minutes and x represents the number of texts sent for each month. Let T represent total cost.
Equation becomes:
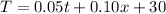
Part B:
Talk (mins)(t) Texts(x)
100 50
124 26
75 75
80 95
50 100
When t = 100 , x = 50

T = $40
When t = 124 , x = 26

T = $38.80
When t = 75 , x = 75
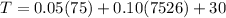
T = $41.25
When t = 80 , x = 95

T = $43.50
When t = 50 , x = 100
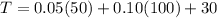
T = $42.50