Question

A 5-cm diameter solid shaft is simultaneously subjected to an axial load of 80 kN and a torque of 400 Nm.

a) Determine the principal stresses at the surface assuming elastic behavior.
b) Find the largest shear stress.

Answer 1

principle stress =46.46 MPa, -5.72 MPa

maximu shear stress 26.08 MPa

Step-by-step explanation:

d = 5 cm = 50 mm

axial load = 80 kN

torque = 400Nm

we know that

axial stress = force/area

`= (80*10^3)/((\pi)/(4) 50^2)`

= 40.74 MPa

shear stress
`= ( Tr)/(J)`

`= (400*10^3 *25mm)/((\pi)/(32)50^4)`

= 16.3 MPa

principle stress is given as

`\sigma_p = (\sigma_a)/(2) \pm \sqrt{ ((\sigma_a)/(2))^2 +z^2}`

`=(40.74)/(2) \pm \sqrt{ ((40.74)/(2))^2 +16.3^2}`

=46.46 MPa, -5.72 MPa

b) maximu shear stress

`\sigma_p = \sqrt{ ((\sigma_a)/(2))^2 +z^2}`

`= \sqrt{ ((40.74)/(2))^2 +16.3^2}`

= 26.08 MPa

Answer 2

principal stress σ = 46.46 MPa and -5.72 MPa

maximum shear stress = 26.08 MPa

Step-by-step explanation:

given data

diameter = 5 cm = 50 mm

axial load = 80 kN = 80000 N

torque = 400 Nm - 400000 N-mm

to find out

principal stresses and shear stress

solution

we find first axial stress that is force / area

axial stress = 80000 / ( π/4×50² )

axial stress σ = 40.74 MPa

and

shear stress = torque × radius / area

shear stress = 400000 × 25 / ( π/4×50² )

shear stress τ = 16.3 MPa

so

principal stress will be

principal stress = σ/2 ±
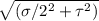`\sqrt{(\sigma/2^(2)+\tau^(2)  )}` ..........1

principal stress σ = 40.74 /2 ±
`\sqrt{(40.74/2^(2)+ 16.3^(2)  )}`

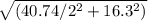
principal stress σ = 46.46 MPa and -5.72 MPa

and

maximum shear stress is

maximum shear stress =
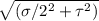`\sqrt{(\sigma/2^(2)+\tau^(2)  )}` ..........2

maximum shear stress =
`\sqrt{(40.74/2^(2)+ 16.3^(2)  )}`

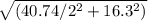
maximum shear stress = 26.08 MPa