Answer:
1
Step-by-step explanation:
Using the Rydberg formula as:
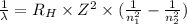
where,
λ is wavelength of photon
R = Rydberg's constant (1.097 × 10⁷ m⁻¹)
Z = atomic number of atom
n₁ is the initial final level and n₂ is the final energy level
For Hydrogen atom, Z= 1
n₂ = 2
Wavelength = 410.1 nm
Also,
1 nm = 10⁻⁹ m
So,
Wavelength = 410.1 × 10⁻⁹ m
Applying in the formula as:

Solving for n₁ , we get
n₁ ≅ 1