Question

A man jogs at a speed of 1.6 m/s. His dog waits 1.8 s and then takes off running at a speed of 3 m/s to catch the man. How far will they have each traveled when the dog catches up with the man? Answer in units of m.

Answer 1

The dog catches up with the man 6.1714m later.

Step-by-step explanation:

The first thing to take into account is the speed formula. It is
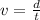`v=(d)/(t)`, where v is speed, d is distance and t is time. From this formula, we can get the distance formula by finding d, it is
`d=v\cdot t`

Now, the distance equation for the man would be:

`d_(man)=v_(man)\cdot t=1.6\cdot t`

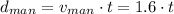
The distance equation for the dog would be obtained by the same way with just a little detail. The dog takes off running 1.8s after the man did. So, in the equation we must subtract 1.8 from t.

`d_(dog)=v_(dog)\cdot (t-1.8)=3\cdot (t-1.8)`

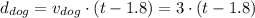
For a better understanding, at t=1.8 the dog must be in d=0. Let's verify:

`d_(dog)=v_(dog)\cdot (1.8-1.8)=3\cdot (0)=0`

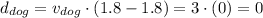
Now, for finding how far they have each traveled when the dog catches up with the man we must match the equations of each one.

`d_(man)=d_(dog)`

`1.6\cdot t=3\cdot (t-1.8)`

`1.6\cdot t=3\cdot t-5.4`

`1.4\cdot t=5.4`

`t=(5.4)/(1.4)`

`t=3.8571s`

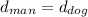
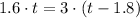
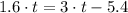
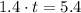
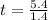
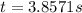
The result obtained previously means that the dog catches up with the man 3.8571s after the man started running.

That value is used in the man's distance equation.

`d_(man)=1.6\cdot t=1.6\cdot (3.8571)`

`d_(man)=6.1714m`

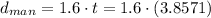
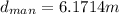
Finally, the dog catches up with the man 6.1714m later.