Question

A Carnot engine whose low-temperature reservoir is at 19.4°C has an efficiency of 29.7%. By how much should the Celsius temperature of the high-temperature reservoir be increased to increase the efficiency to 62.3%?

Answer 1

359.67°C or 359 K

Step-by-step explanation:

Case I:

T2 = 19.4°C = 19.4 + 273 = 292.4 K

η = 29.7 % = 0.297

Let T1 be the temperature of hot reservoir.

By using the formula for the efficiency of Carnot's heat engine

`\eta =1-(T_(2))/(T_(1))`

`0.297 =1-(292.4)/(T_(1))`

`0.703=(292.4)/(T_(1))`

T1 = 415.93 k

Case II:

T2 = 19.4°C = 19.4 + 273 = 292.4 K

η = 62.3 % = 0.623

Let T'1 be the temperature of hot reservoir.

By using the formula for the efficiency of Carnot's heat engine

`\eta =1-(T_(2))/(T_(1))`

`0.0.623 =1-(292.4)/(T'_(1))`

`0.377=(292.4)/(T'_(1))`

T'1 = 775.6 k

Incraese in the temperature of hot reservoir

= T'1 - T1 = 775.6 - 415.93 = 359.67°C or 359 k

Answer 2

The Temperature of the Hot reservoir should be increased by 359.86°C

Step-by-step explanation:

A Carnot engine is a reversible engine, that means that it can work both as a heat engine and as a refrigerator, it can both use heat from a hot reservoir (part of which later must end up in a cold reservoir) to produce work, or use work to move heat from a cod to a hot reservoir.

The efficiency of a carnot engine working as a heat engine is given by:

`\eta = 1 - (T_C)/(T_H)`

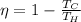
were
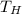`T_H` and
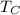`T_C` are the Absolute temperatures of the hot and cold reservoir respectively.

To get the absolute temperature in K from the relative temperature in °C, we must add 273.15 K (the absolute temperature of the freezing point of water at atmospheric pressure)

Thus:

`T_C= 19.4+273.15=292.55 K`

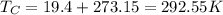
Now, if we know the Temperature of the cold reservoir, and the engine's efficiency, we can use that information to get
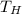`T_H` as follows:

`\eta = 1 - (T_C)/(T_H)\\\eta=0.297\\0.297=1 - (292.55K)/(T_H)\\(292.55K)/(T_H)=1-0.297=0.703\\T_H=(292.55K)/(0.703)=416.14K`

Now, that is the Temperature of the hot reservoir to begin with, but if we want a higher efficency, we need to increase
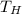`T_H` until
`\eta=0.623`.

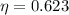To find out what value
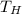`T_H` has to reach, we repeat the same calculation as before, except now
`\eta= 0.623`

`0.623=1 - (292.55K)/(T_H)\\(292.55K)/(T_H)=1-0.623=0.377\\T_H=(292.55K)/(0.377)=776.00K`

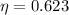
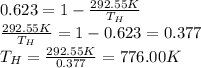
So
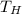`T_H` has increased from
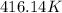`416.14K` to
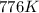`776 K`, that means an increase in temperature of :
`\DeltaT= 776K-416.14K=359.86K`

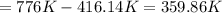
This increment of 359.86K is also an increment of 359.86°C, because increments are relative measures of temperature.