Question

A basketball is dropped from the edge of a cliff at the same time that second basketball is thrown upward from the ground. When they hit each other, the first basketball (the one dropped) has twice the speed of the second one. At what fraction of the height of the cliff does the collision occur?

Answer 1

The collision occurs at a height of 1/3 of the total height of cliff.

Step-by-step explanation:

The situation is represented in the attached figure:

For the stone dropped from top of cliff we have

Initial velocity of drop= 0 m/s.

Now the time at which it attains a velocity of 2v is obtained from first equation of kinematics as

`v_(f)=u_(i)+gt\\\\2v=0+gt\\\\\therefore t=(2v)/(g)`

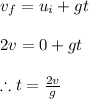
Thus the distance it covers in this time can be calculated using third equation of kinematics as

`v_(f)^(2)=v_(i)^(2)+2gh\\\\(2v)^(2)=2gh_(1)\\\\\therefore h_(1)=(2v^(2))/(g)`

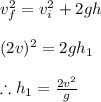
For the stone thrown upwards the velocity at collision is give as 'v' thus the velocity at which it is thrown upwards can be calculated by first equation of kinematics as

`v=v_(i)-gt\\\\\therefore v_(i)=v+gt\\\\v_(i)=v+g* (2v)/(g)\\\\\therefore v_(i)=3v`

The height over which it changes it's velocity from '3v' to 'v' can be again obtained from third equation of kinematics as

`v^(2)=(3v)^(2)-2gh_(2)\\\\v^(2)=9v^(2)-2gh_(2)\\\\\therefore h_(2)=(4v^(2))/(g)`

`\therefore h_(2)=2h_(1)`

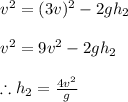
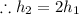
Thus the collision occurs at at a fraction of 1/3 of height.