Answer:
a)
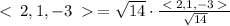
b)
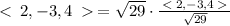
c)

Explanation:
a) Let a=<2,1,-3>
The magnitude of a is
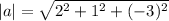
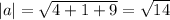
The unit vector in the direction of a is
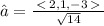
Using the relation
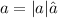 , we have
, we have
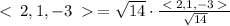
b) Let a=2i - 3j + 4k
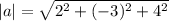

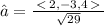
Using the relation
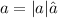 , we have
, we have
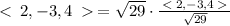
c) Let us first find the sum of <1, 2, -3> and <2, 4, 1> to get:
<1+2, 2+4, -3+1>=<3, 6, -2>
Let a=<3, 6, -2>
The magnitude is
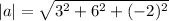
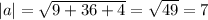
The unit vector in the direction of a is

Using the relation
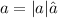 , we have
, we have
