Question

Let S be the closed surface that consists of the hemisphere x2 + y2 + z2 = 1, z ≥ 0, and its base x2 + y2 ≤ 1, z = 0. Let E be the electric field defined by E(x, y, z) = 2xi+ 2yj + 2zk. Find the electric flux across S.

Answer 1

`F=4\pi`

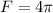
Step-by-step explanation:

The total surface is composed of two surfaces:

`S=S_(1)+S_(2)`

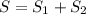
S1: x2 + y2 + z2 = 1, z ≥ 0

S2: x2 + y2 ≤ 1, z = 0

On the other hand the electric field has a radial direction:

E(x, y, z) = 2xi+ 2yj + 2zk=2(x,y,z)=2r

r: is the vector radial (x,y,z)

Flux across S1:

The Surface is a semi sphere with radius equal 1, then the direction from a differential of surface (dS) is also radial. In other words the electric field has the same direction as the Surface for all x, y and z, so the Flux is:

`F_(1)=\int\limits^. {E} \, dS`

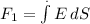
E at the surface, semi sphere with radius equal 1

E=2r=2u (u: vector unitaire radial)

Its magnitude

E=2

So:

`F_(1)=\int\limits^. {E} \, dS=E\int\limits^. \, dS=ES=E*(2\pi*R^(2))=4\pi`

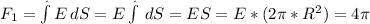
Flux across S2:

The surface is part of z=0, its direction is always (0,0,1). The electric field is radial, so at this surface the electric field direction will be over the surface. We can observe that the surface is always perpendicular to the champ electric at this surface, so the Flux is zero.

Total Flux:

`F=F_(1)+F_(2)=4\pi`