Answer:
The equation for circle of radius
 centered at the point
centered at the point
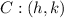 is:
is:

Explanation:
To derive this equation, we need the formula for the distance between two points in the plane. If the point is given by its cartesian coordinates, we can use the Pythagorean theorem to find what the distance between the points is.
Lets say we have two points, one given by cartesian coordinates P:(x,y) and the other given by cartesian coordiantes C:(h,k)
(see diagram)
We can see that
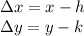
and by the pythagorean theorem we have:
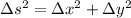
Where
 is the distance between the points
is the distance between the points
Now, combining the last three equations we find:
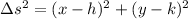
We know that the definition of a circle is the locus of points that are at a distance r from a point called the center of the circle. if we take C:(h,k) as the center of the circle, and
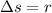 , the last equation becomes:
, the last equation becomes:
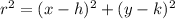
And that is the result we wanted.