Question

IQ scores are known to be normally distributed. The mean IQ score is 100 and the standard deviation is 15. The top 25% of the population (ranked by IQ score) have IQ’s above what value?

Answer 1

110

Explanation:

We have been given that the mean IQ score is 100 and the standard deviation is 15.

We will use normal distribution table to solve our given problem.

The top 25% of the population will represent scores greater than 75%.

The z-score corresponding to data greater than 75% is 0.6745.

Upon substituting our given values in z-score formula, we will get:

`z=(x-\mu)/(\sigma)`

`0.6745=(x-100)/(15)`

`0.6745*15=(x-100)/(15)*15`

`10.1175=x-100`

`10.1175+100=x-100+100`

`110.1175=x`

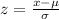
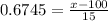
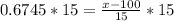
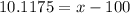
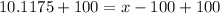
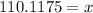
Therefore, the top 25% of the population (ranked by IQ score) have IQ’s above 110.