Question

A 4-person task force is to be formed from the 4 men and 3 women who work in Company G’s human resources department. If there are to be 2 men and 2 women on this task force, how many different task forces can be forme?

Answer 1

Total 18 task force can be formed.

Explanation:

Total number of men = 4

Total number of women = 3

We need to form a 4-person task force.

The total number of ways of selecting r items from n items is

`^nC_r=(n!)/(r!(n-r)!)`

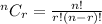
Total number of ways of selecting 2 men from 4 men =
`^4C_2`

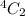
Total number of ways of selecting 2 women from 3 men =
`^3C_2`

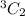
Total number of different task forces that can be formed is

`Total=^4C_2* ^3C_2`

`Total=(4!)/(2!(4-2)!)* (3!)/(2!(3-2)!)`

`Total=(4!)/(2!2!)* (3!)/(2!1!)`

`Total=(4* 3* 2!)/(2* 1* 2!)* (3\tmes 2!)/(2!)`

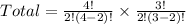
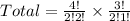
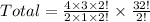
Cancel out common factors.

`Total=6* 3`

`Total=18`

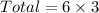
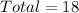
Therefore total 18 task force can be formed.