Question

Two small plastic spheres are given positive electrical charges. When they are a distance of 14.8cm apart, the repulsive force between them has a magnitude of 0.235 N.

What is the charge on each sphere if the two charges are equal?
What is the charge on first sphere if it has four times the charge of the other?
What is the charge on the second sphere?

Answer 1

The charge on each sphere is approximately +/- 4.87 x 10^-6 C when they are equal. The charge on the first sphere is approximately +/- 1.95 x 10^-5 C if it has four times the charge of the second sphere. The charge on the second sphere is approximately +/- 4.87 x 10^-6 C.

Step-by-step explanation:

To find the charge on each sphere when they are equal, we can use Coulomb's Law. Coulomb's Law states that the force between two charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. Mathematically, it can be represented as:

Force = (k * charge1 * charge2) / distance^2

Given that the force is 0.235 N and the distance between the spheres is 14.8 cm, we can plug these values into the equation and solve for the charges:

0.235 = (k * charge^2) / (0.148^2)

where k is the proportionality constant in Coulomb's Law. Solving this equation, we find that the charge on each sphere is approximately +/- 4.87 x 10^-6 C.

To find the charge on the first sphere if it has four times the charge of the second sphere, we can use the same equation:

0.235 = (k * (4 * charge)^2) / (0.148^2)

Simplifying this equation, we find that the charge on the first sphere is approximately +/- 1.95 x 10^-5 C.

Since the charge on the first sphere is four times the charge on the second sphere, the charge on the second sphere is approximately +/- 4.87 x 10^-6 C.

Answer 2

Step-by-step explanation:

Case I: They have same charge.

Charge on each sphere = q

Distance between them, d = 14.8 cm = 0.148 m

Repulsive force, F = 0.235 N

Use Coulomb's law in electrostatics

`F=(Kq_(1)q_(2))/(d^(2))`

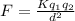
By substituting the values

`0.235=(9*10^(9)q^(2))/(0.148^(2))`

`q=7.56*10^(-7)C`

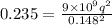
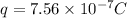
Thus, the charge on each sphere is
`q=7.56*10^(-7)C`.

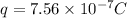Case II:

Charge on first sphere = 4q

Charge on second sphere = q

distance between them, d = 0.148 m

Force between them, F = 0.235 N

Use Coulomb's law in electrostatics

`F=(Kq_(1)q_(2))/(d^(2))`

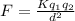
By substituting the values

`0.235=(9* 10^(9)* 4q^(2))/(0.148^(2))`

`q=3.78*10^(-7)C`

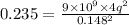
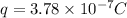
Thus, the charge on second sphere is
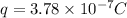`q=3.78*10^(-7)C` and the charge on first sphere is
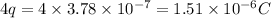`4q = 4* 3.78* 10^(-7)=1.51 * 10^(-6) C`.