Question

Sketch the electric field around these two objects if they have the same sign of charge. Make a separate drawing showing equipotential lines around the two charges. The potential is defined to be zero at infinity. Identify the line of zero potential between the two charges, if there is one.

Answer 1

* far from one of the charges, the field of the other charge is small and can be neglected

* on the outside of the loads the fields are added territorially

* between the charges the two fields tend to vanish

Step-by-step explanation:

The electric field around two objects with charge of the same sign, for simplicity suppose that the objects have positive point spherical charges,

E = k q / r2

bold letters indicate vectors, therefore the total electric field is

E_total = E1 + E2

the module of this field is

E_total = E1- E2

therefore we can outline this field

* far from one of the charges, the field of the other charge is small and can be neglected

* on the outside of the loads the fields are added territorially

* between the charges the two fields tend to vanish

An outline of these shows in Attachment A

The equipotential surfaces are defined as being perpendicular to the electric field lines since the electric field and the power difference are related

E =
`(dV)/(dx) i^ + (dV)/(dy) j^ + (dV)/(dz) k^ = \Delta V`

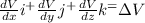
We can schematize some characteristics of these surfaces

* very close to each load are spherical surfaces

* very far from the load is an elliptical surface, which envelops the loads

* between them there is a point of zero potential point C

See attached part B