Answer:
The function that represents the amount of air is
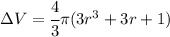
Explanation:
The amount of air here represents the difference between V(r) and V(r+1), so we can start working by finding an expression for the volume at r+1, and then subtract the original volume V(r).
Volume of balloon of radius r+1 inches.
We can replace r with r+1 on the formula and we get:
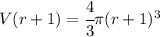
We can expand
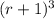 since we will use it to simplify it later on.
since we will use it to simplify it later on.
So we will have first
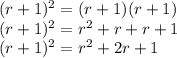
We can multiply that result by (r+1) to get
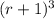
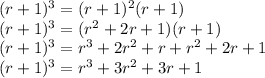
Thus the volume equation at r+1 will be
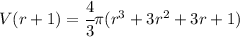
Finding the amount of air required to inflate from r to r+1
The amount required to inflate is the difference of volumes, so we have
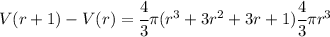
Combinging both into one term by factor
 give us
give us
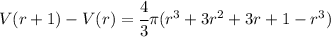
Simplifying
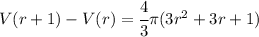
And that function represents the amount required to inflate the balloon from r to r+1 inches.