Question

Quick Sell Outlet sold a total of 40 televisions, each of which was either a Model P television or a Model Q television. Each Model P television sold for $p and each Model Q television sold for $q. The average (arithmetic mean) selling price of the 40 televisions was $141. How many of the 40 televisions were Model P televisions?

Answer 1

`(5640-40p)/(p-q)`

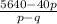
Explanation:

Here, the total number of television = 40,

Let x be the number of P television,

So, the number of Q television = (40 - x)

Now, the price of each P television is $ p,

∴ The total price of P televisions = xp dollars,

Also, the price of each Q television is $ q,

∴ The total price of Q televisions = (40-x)q dollars,

Thus, the total price of 40 television = xp + (40-x)q = x(p-q) + 40q,

Hence, the average price =
`\frac{\text{Total price}}{\text{Number of television}}`

`=(x(p-q)+40q)/(40)`

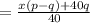
According to the question,

`(x(p-q)+40q)/(40)=141`

`x(p-q)+40q=141* 40`

`x(p-q) = 5640 - 40q`

`\implies x=(5640-40p)/(p-q)`

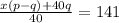
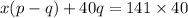
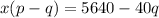
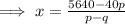
Therefore, there were
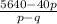`(5640-40p)/(p-q)` P model televisions.