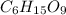Answer: The molecular formula will be
Step-by-step explanation:
If percentage are given and we are given total mass is 100 grams.
So, the mass of each element is equal to the percentage given.
Mass of C= 31.17 g
Mass of H = 6.54 g
Mass of O = 62.29 g
Step 1 : convert given masses into moles.
Moles of C =
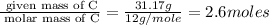
Moles of H=
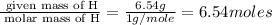
Moles of O =
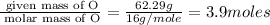
Step 2 : For the mole ratio, divide each value of moles by the smallest number of moles calculated.
For C=
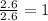
For H =
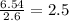
For O =
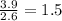
The ratio of C: H: O= 1: 2.5: 1.5
Converting them into whole number ratios by multiplying by 2.
Hence the empirical formula is
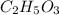
The empirical weight of
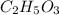 = 2(12)+5(1)+3(16)= 77 amu
= 2(12)+5(1)+3(16)= 77 amu
The molecular weight = 231.2 amu
Now we have to calculate the molecular formula.

The molecular formula will be=
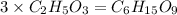
The molecular formula will be